Depth profiles

Vincent Godard

2022-10-06

Introduction

How to use this document?

This html page is derived from an R Markdown Notebook. You can copy/paste the various lines of code into your own R script and run it in any R session.

Objectives

The objective of this notbook is to illustrate simple computations on depth profiles.

Setup

The first thing we have to do is to load the TCNtools library (once it has been installed)

library("TCNtools")

We will need some parameters concerning production rates, attenuation length, etc …

data(Lambda) # we load a vector containing the attenuation length into the environment (g/cm2)
data(prm) # we load a matrix containing the production/decay parameters into the environment

Loading a dataset

The package TCNtools includes a selection of depth profiles data from the literature. We will use the profile from Laloy et al. (2017).

data("tcn_depth_profiles") # import the data set
data = tcn_depth_profiles[tcn_depth_profiles$study=="laloy2017bayesian",] # selecting a particular study

We can then compute the scaling for this study site. Note that each site characteristics are only reported for the first sample (label=1).

altitude = data$altitude[1] # elevation in m
latitude = data$latitude[1] # latitude in degrees
P = atm_pressure(alt=altitude,model="stone2000") # compute atmospheric pressure at site
S = scaling_st(P,latitude) # compute the scaling parameters according to Stone (2000)

We can plot the data.

plot(NA,xlim=range(data$C,50e3,200e3),ylim=rev(range(data$depth)),
     xlab="10Be concentration (at/g)",ylab="Depth below surface (cm)")
grid()
arrows(data$C-data$C_e,data$depth,data$C+data$C_e,data$depth,length = 0)
points(data$C,data$depth,pch=21,cex=2,bg="pink")
text(data$C,data$depth,data$label,cex=0.7)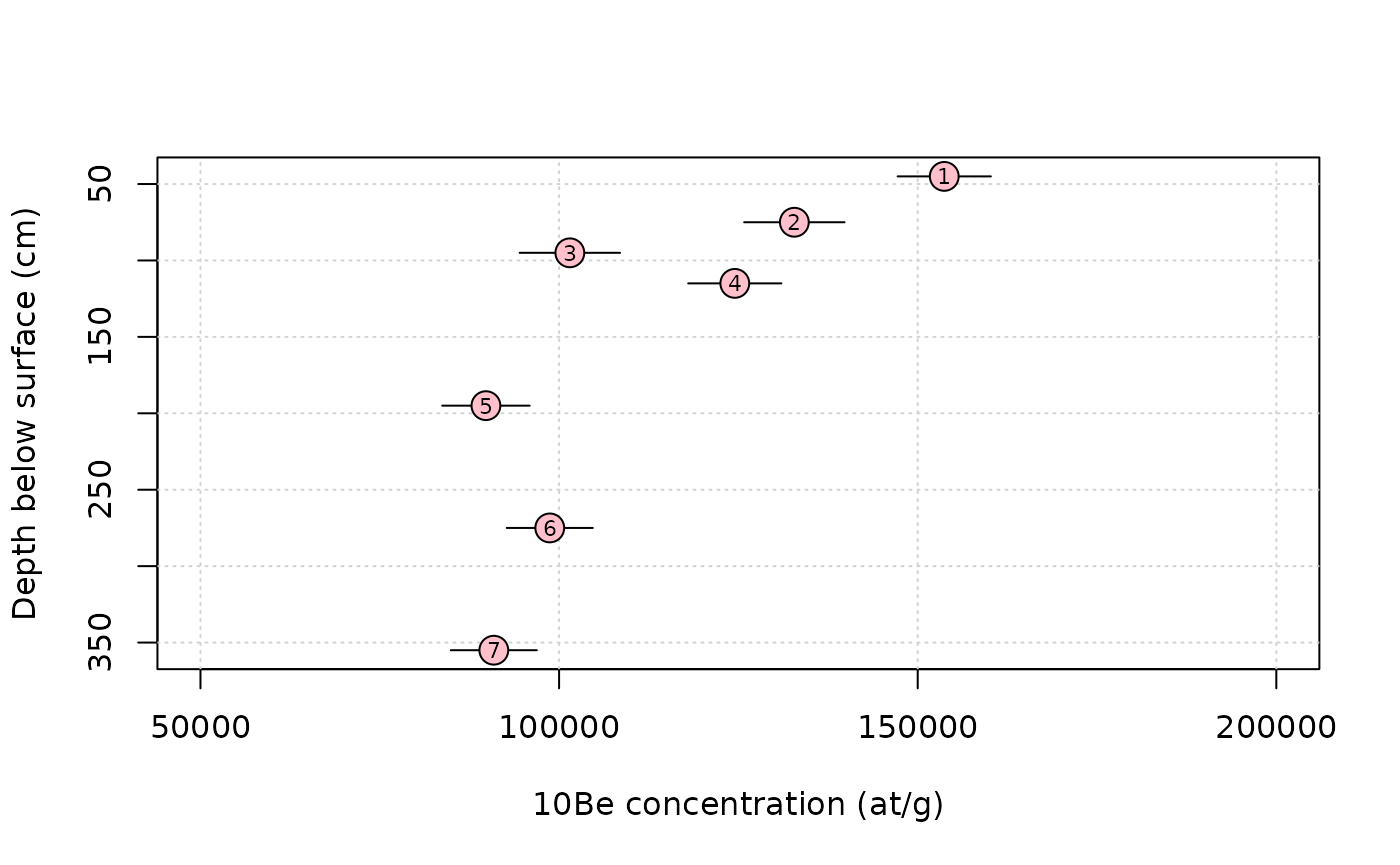

Then we can compute a theoretical profile for a guess of the value for the parameters

rho = 1.7 #  density (g/cm3)
ero = 40*100/1e6*rho  # m/Ma -> g/cm2/a
age = 0.4e6 # a
C0 = 80e3 # inheritance (at/g)
z = seq(0,max(data$depth),length.out = 40)*rho # calculation depth (g/cm2)
C = solv_conc_eul(z,ero,age,C0,prm[,"Be10"],S,Lambda) # compute concentration´

We now plot the results.

plot(NA,xlim=range(data$C,50e3,200e3),ylim=rev(range(data$depth)),
     xlab="10Be concentration (at/g)",ylab="Depth below surface (cm)")
grid()
lines(C,z,lwd=3) # plotting the modelled profile
arrows(data$C-data$C_e,data$depth,data$C+data$C_e,data$depth,length = 0)
points(data$C,data$depth,pch=21,cex=2,bg="pink")
text(data$C,data$depth,data$label,cex=0.7)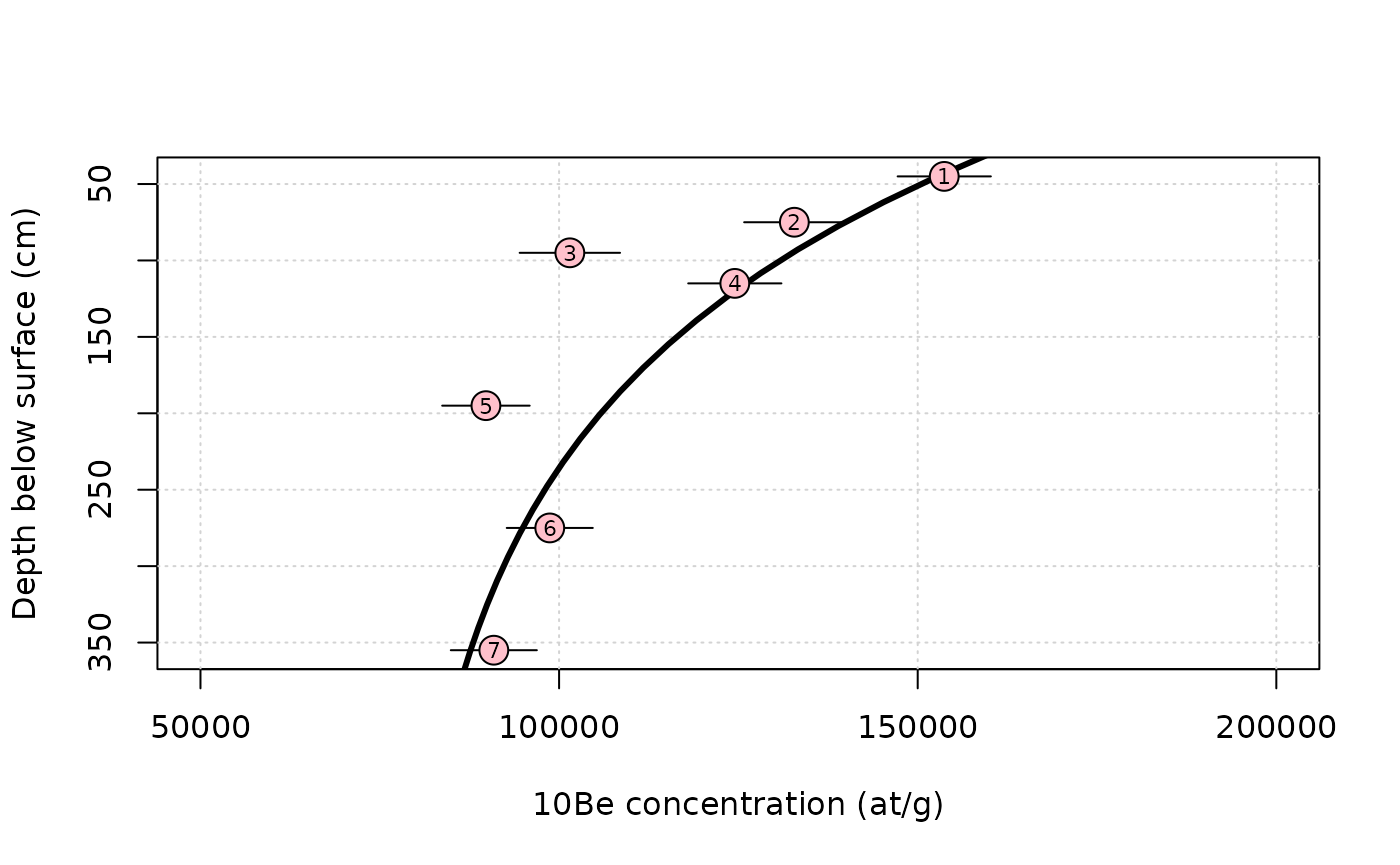

Exploring the parameters space

Preliminary exploration

We could change the parameters incrementally one by one to explore the effects on the modeled profile and attempt to converge toward a best-looking solution. It is obviously much more efficient and robust to do this automatically by going through a large number of parameters sets, compute the predicted concentrations (\(C_{mod}\)) and evaluate how well they match the observed concentrations (\(C_{obs}\) with uncertainty \(\sigma\)). We can use the \(\chi^2\) to quantify the difference between the model and observations.

\[\begin{equation} \chi^2 = \sum_{i=1}^n \left( \frac{C_{obs,i} - C_{mod,i} }{\sigma_i} \right)^2 \end{equation}\]

The function depth_profile_mc will allow us to generate a large number of models over the parameter space defined by :

  • the age of the formation (age in a)
  • the surface denudation rate (ero in m/Ma)
  • the inherited concentration (inh in at/g)
  • the density (rho in g/cm2)

There two additional parameters n1 and n2, which control how many models we are going to sample from this paramters space

  • n1 is the number of model which are randomly drawn (Monte Carlo)
  • n2 is the number of regularly sampled points for each parameter (si if all 4 parameters are varying the number of models is n2\(^4\))

We can choose to carry out an exploration of the parameters space which completely random (n2=0) or following a regular grid (n1=0), or a combination of both.

This first attempt is a crude exploration of the parameter space.

res = depth_profile_mc(data$C,data$C_e,data$depth,prm[,"Be10"],Lambda,S,
                       age=c(0,100)*1000,
                       ero=c(0,50),
                       inh=c(0,1)*1e5,
                       rho=c(1.5,2.5),
                       n1=2000,n2=15)

Note that in depth_profile_mc we could choose to fix a parameter by passing a single value as argument, instead of a two elements vector, which corresponds to the bounds of the explored interval.

We can have a look at the result table.

summary(res)
##       age              ero             inh              rho       
##  Min.   :     0   Min.   : 0.00   Min.   :     0   Min.   :1.500  
##  1st Qu.: 21429   1st Qu.:10.71   1st Qu.: 21429   1st Qu.:1.714  
##  Median : 50000   Median :25.00   Median : 50000   Median :2.000  
##  Mean   : 50012   Mean   :25.02   Mean   : 49991   Mean   :2.000  
##  3rd Qu.: 78571   3rd Qu.:39.29   3rd Qu.: 78571   3rd Qu.:2.286  
##  Max.   :100000   Max.   :50.00   Max.   :100000   Max.   :2.500  
##       chi2        
##  Min.   :  13.07  
##  1st Qu.: 102.70  
##  Median : 331.62  
##  Mean   : 495.69  
##  3rd Qu.: 761.88  
##  Max.   :2848.55

Based on the \(\chi2\) value we can now try to have a look at a subset of our model, which correspond to the best fitting values for this metric. We can start to do that very coarsely by looking at a quantile, for example the best 1%.

cutoff = quantile(res$chi2,0.01)
best = res[res$chi2<cutoff,]
pairs(best[,-5],pch=16,col=adjustcolor("blue",0.2)) # we remove the last column (5) which correspond to the chi2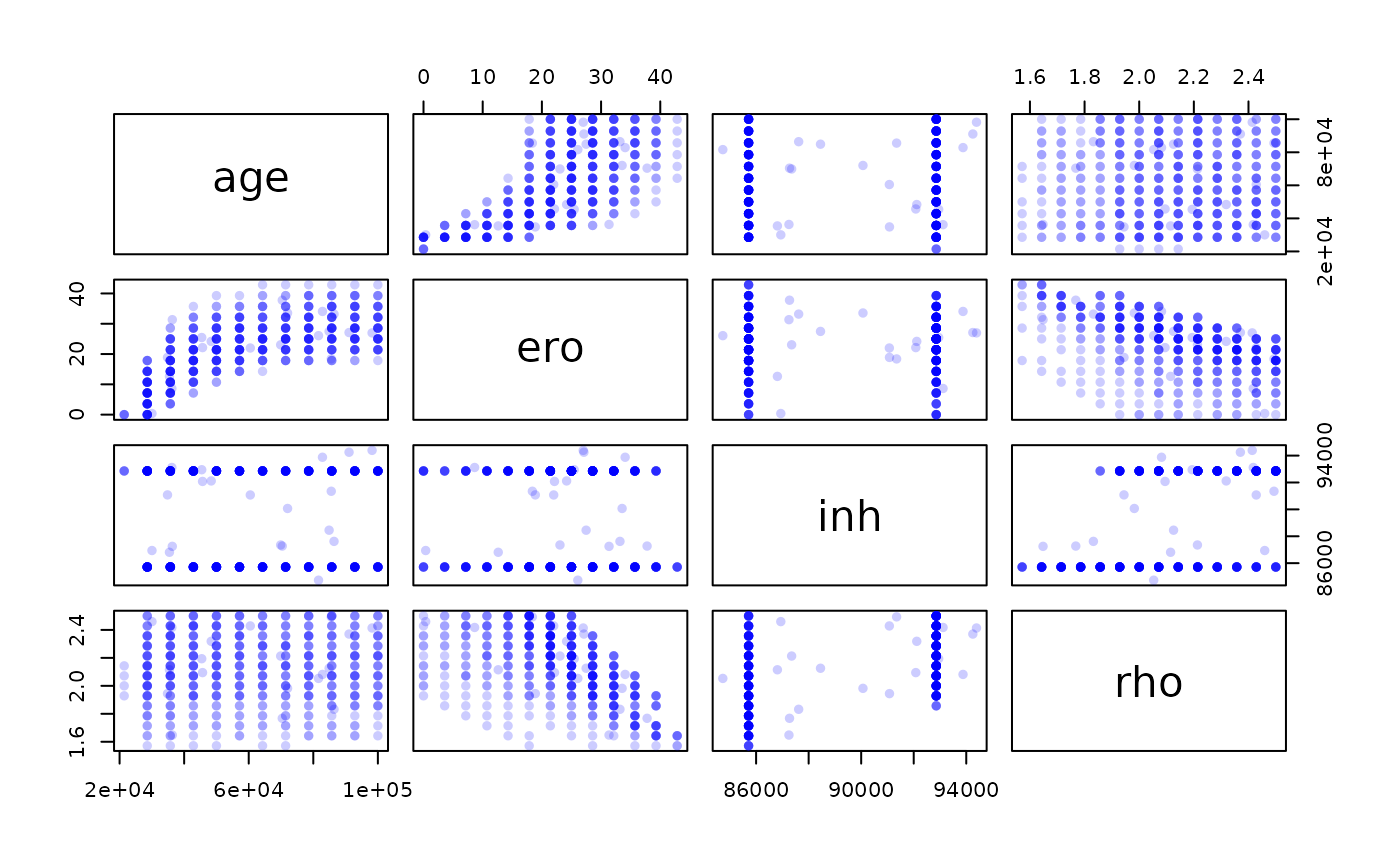

We see numerous tradeoffs between parameters, notably between age and denudation rate.

We can also select and plot the best model

imin = which.min(res$chi2) # position of the lowest chi2 in the dataframe
z = seq(0,max(data$depth),length.out = 40) # calculation depth (g/cm2)
C = solv_conc_eul(z*res$rho[imin],res$ero[imin]*100/1e6*res$rho[imin],res$age[imin],res$inh[imin],prm[,"Be10"],S,Lambda) # compute concentration
#
plot(NA,xlim=range(data$C,50e3,200e3),ylim=rev(range(data$depth)),
     xlab="10Be concentration (at/g)",ylab="Depth below surface (cm)")
grid()
lines(C,z,lwd=3) # plotting the modeled profile
arrows(data$C-data$C_e,data$depth,data$C+data$C_e,data$depth,length = 0)
points(data$C,data$depth,pch=21,cex=2,bg="pink")
text(data$C,data$depth,data$label,cex=0.7)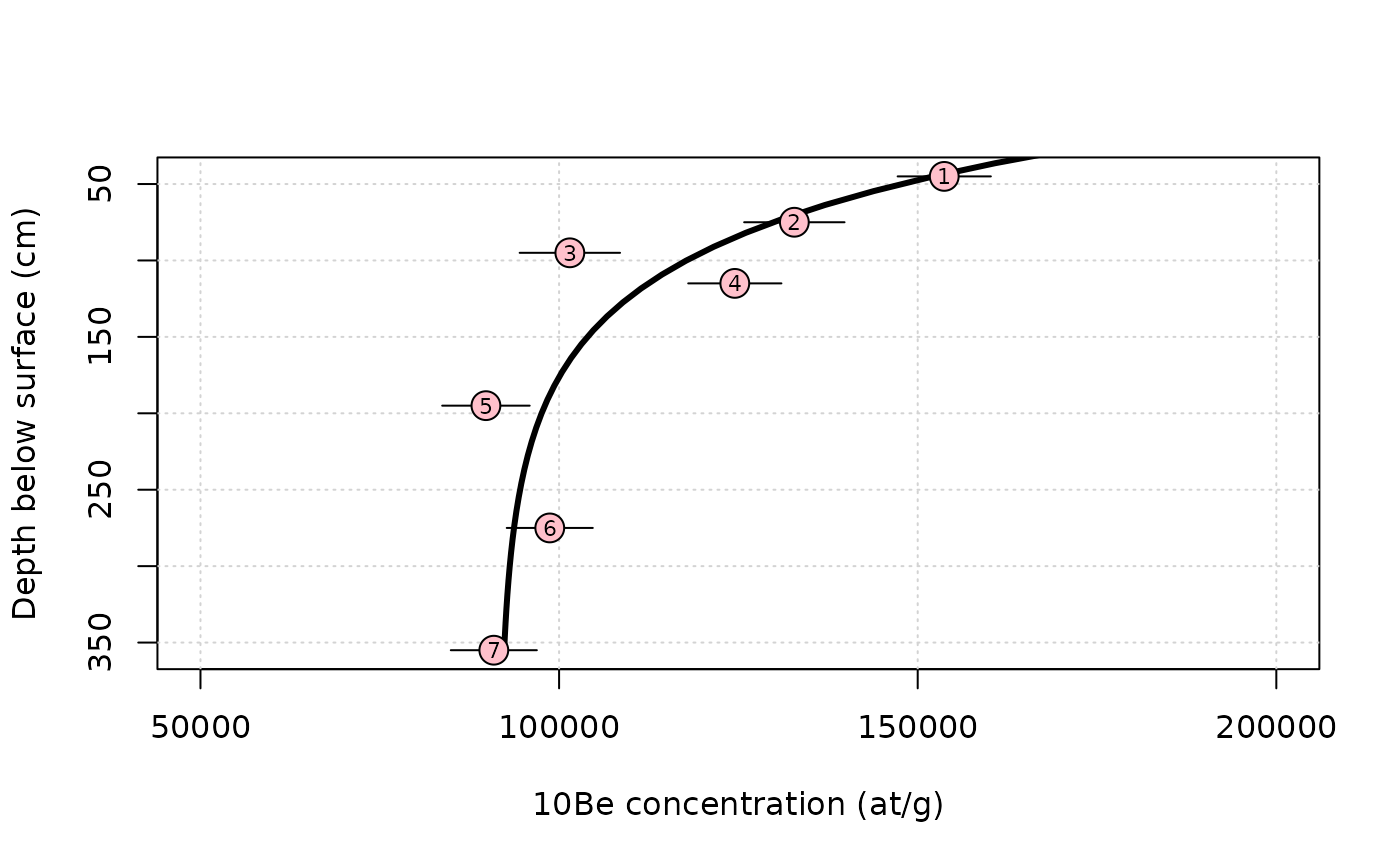

In many situation we have some knowledge about the value or plausible ranges of some parameters. For example the density can be measured at teh sampling site, and inheritance can be estimated from the shape of the profile, in our case it seems reasonable to consider that it is close to 90\(\times10^3\) at/g. We can restrict the range of variation or even fix these parameters, which what we do next, by letting only the age and denudation rate as free parameters. In this case the results will be much easier to visualize through the construction of a \(\chi^2\) surface.

res = depth_profile_mc(data$C,data$C_e,data$depth,prm[,"Be10"],Lambda,S,
                       age=c(0,100)*1000,
                       ero=c(0,50),
                       inh=90*1e3,
                       rho=2,
                       n1=20000,n2=20)
cutoff = quantile(res$chi2,0.01)
best = res[res$chi2<cutoff,]
plot(best$ero,best$age/1000,pch=16,col=adjustcolor("blue",0.2),
     xlab="Denudation rate (m/Ma)",ylab="Age (ka)")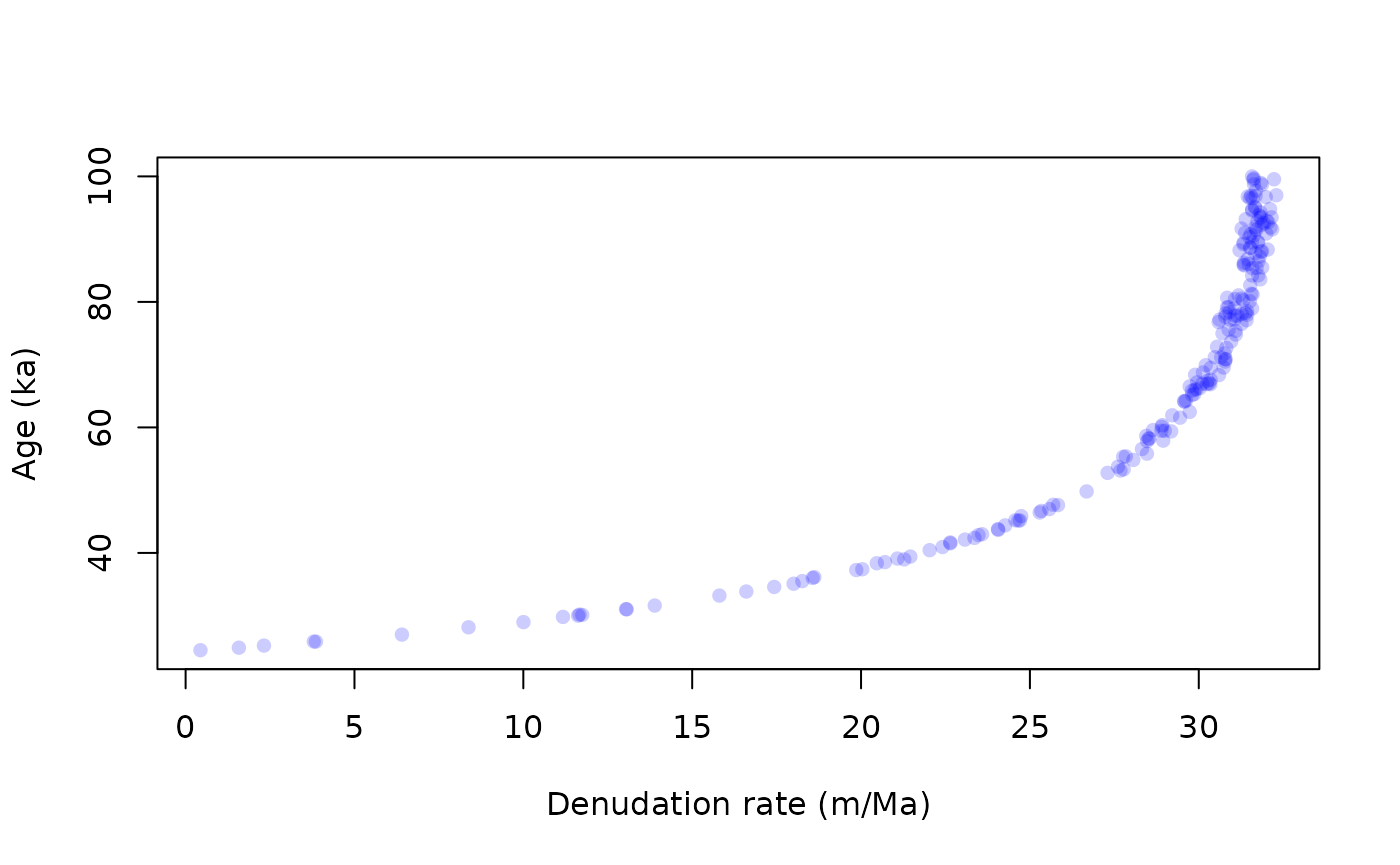

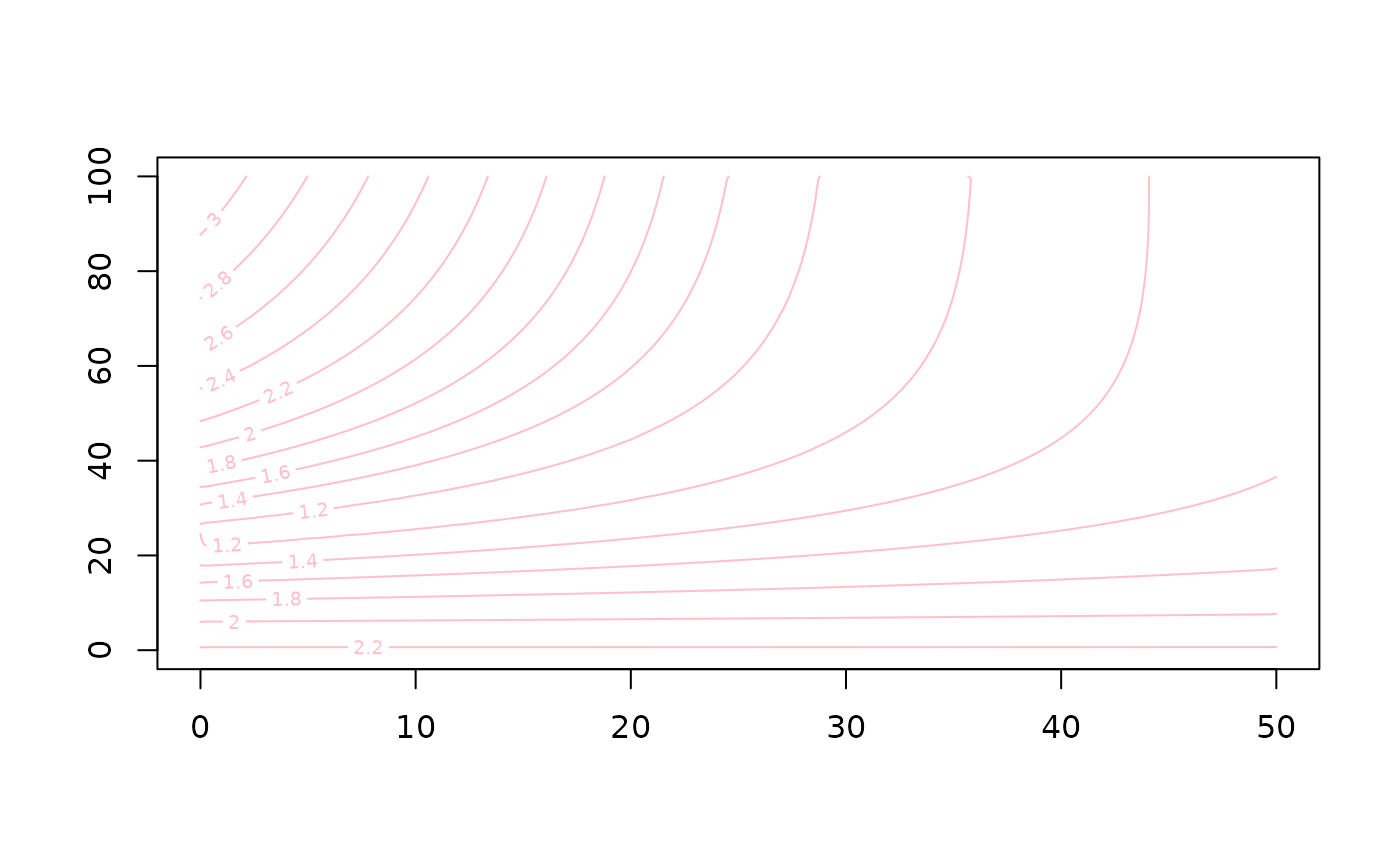
Alternatively we can represent the results as a continuous \(\chi^2\) surface. We use the library akimas to grid the results, note that .

library("akima")
spline<-interp(res$ero/max(res$ero),res$age/max(res$age),log10(res$chi2),duplicate="mean",nx=200,ny=200)
contour(spline$x*max(res$ero),spline$y*max(res$age)/1e3,spline$z,col="pink")

References

Laloy, Eric, Koen Beerten, Veerle Vanacker, Marcus Christl, Bart Rogiers, and Laurent Wouters. 2017. “Bayesian Inversion of a CRN Depth Profile to Infer Quaternary Erosion of the Northwestern Campine Plateau (NE Belgium).” Earth Surface Dynamics 5 (3): 331–45. https://doi.org/gcc5fn.